Lecture 3 Loss Functions and Optimization

We didn’t know how to choose W while using linear classification(regression): Define loss function and find the method to minimize(optimize) given loss function

• Loss function: given data $\{(x_i, y_i)\}_{i=1}^N$ and prediction function f(x, W), loss function is $L = \frac{1}{N} \sum_i L_i(f(x_i, W), y_i)$ and it would quantitize the error of the gap between prediction and real value.

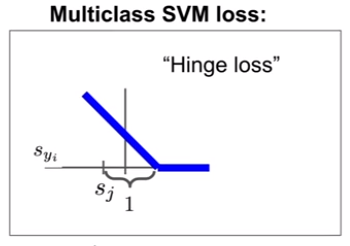
• multiclass SVM with hinge loss:

  • hinge loss has a meaning that ‘if score of right category is large enough(> 1), then loss is zero, we do not correct the parameter for minimizing loss of that right picture’
  • hinge loss also has a meaning that ‘if score of right category is not large enough (< 1), then loss is given as linear’
  • constant 1 means ‘invariant with scale(or, even though we choose any constant, it would be cancelled with scale)’
  • there also exists the quadratic form of hinge loss; the usage of both is depending on the problem and we should consider the tradeoffs of each form. (For example if we use quadratic form of hinge loss, then we care more about the large mis-classification error, but if the score between right category and incorrect category are small, then the size of loss is much smaller.)
  • W* s.t. loss is zero is not unique. (by scale-invariant, and zero loss range) $\begin{matrix} L_i &=& \sum_{j \neq y_i} \begin{cases} 0 & if \; s_{y_i} \geq s_j + 1 \\ s_j - s_{y_i} +1 & otherwise \end{cases} \\ \\ &=& \sum_{j \neq y_i} max(0, s_j - s_{j_i} +1 ) & \quad & \quad \end{matrix}$

• multiclass SVM with Softmax Classifier:
  • exponential, then normalize by making probability of each category. $\begin{matrix} P_i &=& \frac{e^{s_{yi}}}{\sum_j e^{s_j}} \\ L_i &=& - log( P_i ) \end{matrix}$

• Regularization Method: Based on Occam’s Razor axiom(Among competing hypotheses, the simplest is the best)
  • Regularizaiton Method: Giving a penalty on high-degree coefficient
    • lambda(hyperparameter, regularization strength) determines what value we care more;
      • if lambda is large enough, then loss value of each data goes zero effect(underfitting).
      • if lambda is about zero, then the prediction function would be fitted to wiggy curve satisfying only train data(overfitting).
    • commonly used regularization is L2, L1, Elastic net(L1+L2), Max norm regularization, Dropout, Batch normalization, Stochastic depth, else.
  • Strict Method: Choosing a model with low-degree polinomial $L(W) = \frac{1}{N} \sum_i^N L_i(f(x_i, W), y_i) + \lambda R(W)$ $\begin{matrix} R_{L2}(W) &=& \sum_k\sum_l W_{k,l}^2 \\ R_{L1}(W) &=& \sum_k\sum_l \left| W_{k,l} \right| \\ R_{ElasticNet}(W) &=& \sum_k\sum_l (\beta W_{k,l}^2 + \left| W_{k,l} \right|) \end{matrix}$

• Optimization Method
  • Random Walk Method(No Good at all)
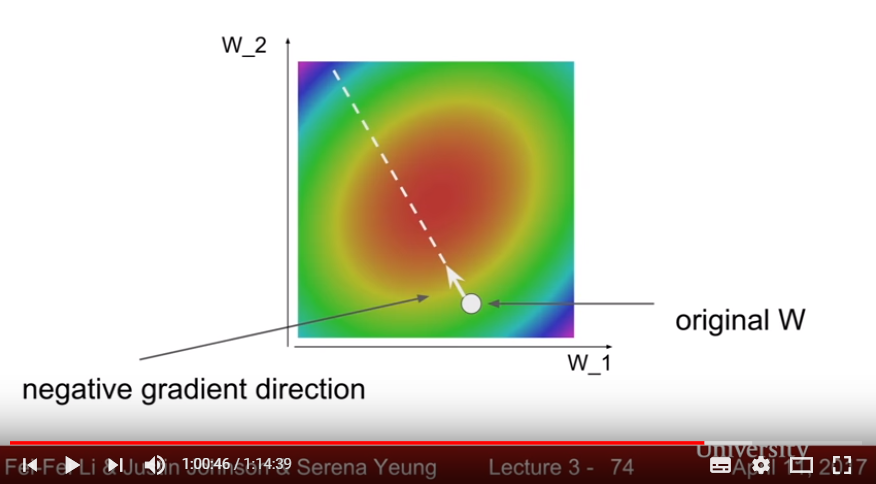
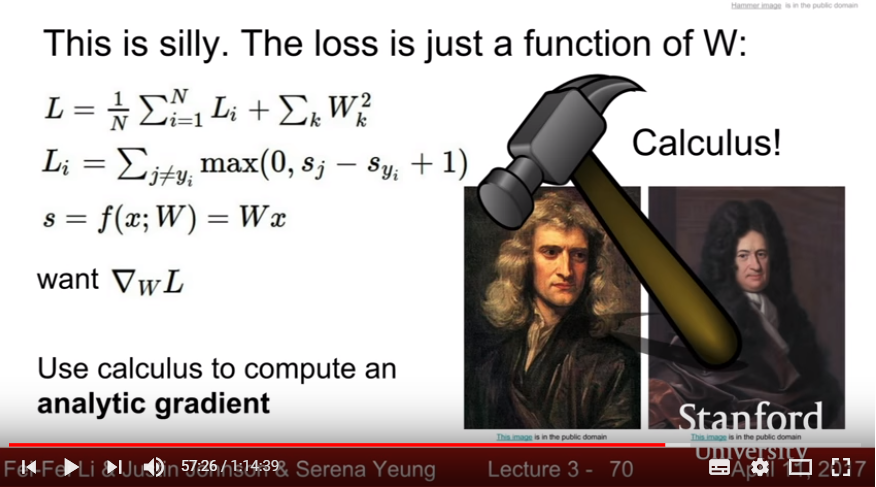
  • Gradient Discent: Using local geometry of surface - solve partial derivative of L(W), then iterate a small step change to each parameters in a way reduces the loss
    • Numerical Gradient: Easy to write and understand, but slow and not good for aproximate
    • Analytic Gradient(using partial derivative): Fast and Exact, but not error-prone
  • Stochastic Gradient Discent: Instead of summing all loss of N train data, use minibatch of 32/64/128 train data to compute gradient discent.
    • We use the sum of minibatch as the estimation of sum of all data; Monte Carlo Estimation of sum value, that means Stochastic Method

• Linear Classification has limitation in recognizing image; Alternations
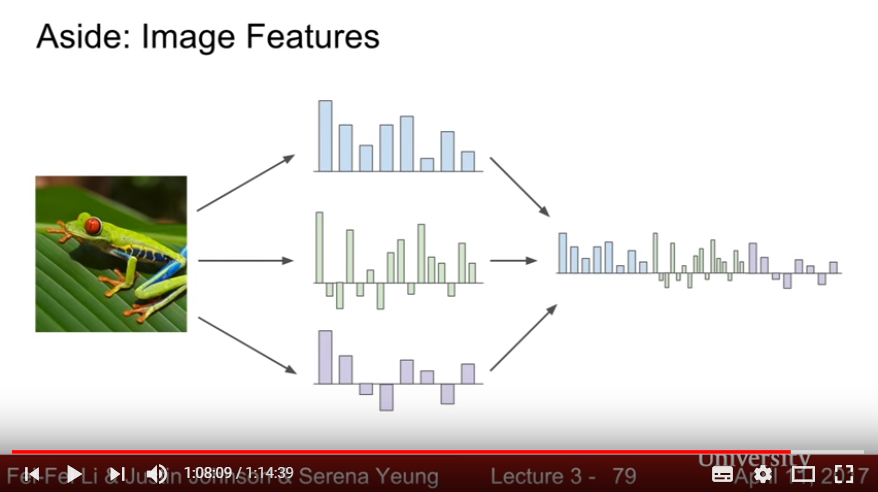
  • Finding Image Features: featuring various representations then classify with each features(Consider feature Transformation, or changing basis with not each pixel but separated feature)
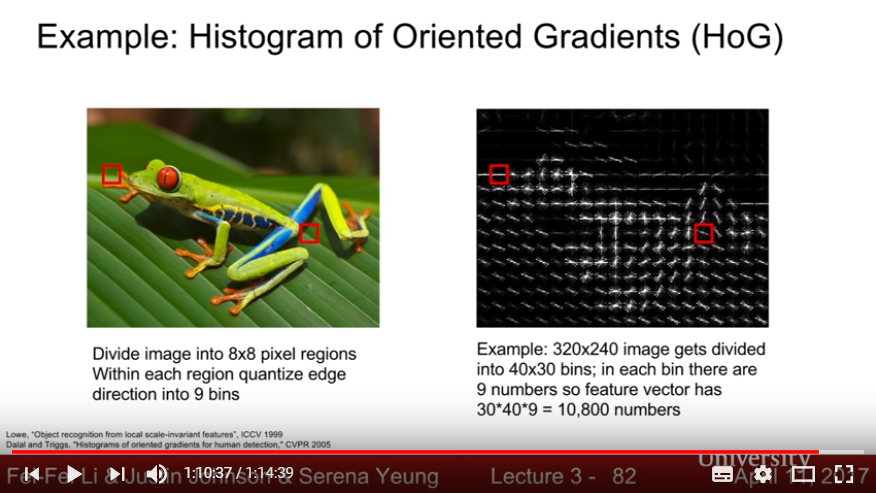
    • Histogram of Oriented Gradients: divide picture into each bin, and find the feature(edge) in each bins
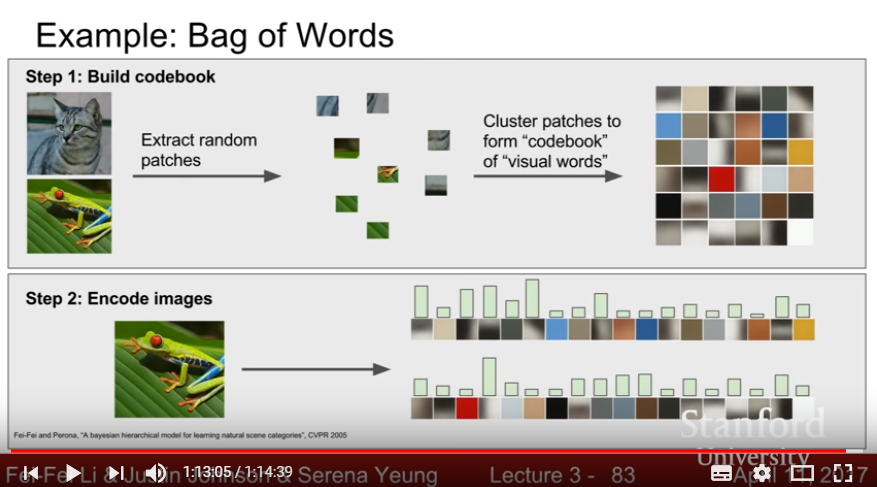
  • Bag of words: Extract each image to random patches, cluster it with bunch of codebook and encode image with appearance of each codebooks